構造物の損傷・破壊過程を再現するシミュレーション技術の開発

プログラムの概要

数値震動台では、ソリッド要素を用いた詳細有限要素モデルを用いるため、解くべき連立一次方程式は数百万～数千万自由度の大規模問題となります。数値震動台ではADVENTURECluster（以下、ADVC）をプラットフォームに採用しています。 ADVCは収束性の良いCGCG法による並列ソルバーを有しており、数百万自由度以上の複雑形状の大規模構造問題を高速に解くことができます。接線剛性の計算や応力の計算は、材料毎に数理モデルや計算アルゴリズムが異なるため独自の開発が必要となります。これまでに数値震動台で開発している材料モデルの一覧を以下に示します。

材料	構成則	主な適用事例
鋼材	semi-implicit型ルールを用いた区分線形複合硬化モデル	4層鋼構造建物
コンクリート	前川構成則 PDS-FEM	RC橋脚
コンクリート	圧壊およびクラックを考慮した拡張Drucker-Prager則	CFT柱 10層RC建物
天然ゴム高減衰ゴム	Ogdenモデル粘超弾性モデル	高減衰ゴム免震支承
地盤	下負荷面ECモデル	地盤地中構造物

鋼材構成則

鋼材構成則について、鋼材料の繰り返し特性を考慮する構成則として、Bounding Surface、 Multi-surface、Armstrong-Frederic modelなど多く提案されています。しかし、これらの構成則は複雑であることから、非線形有限要素解析ではNewton-Raphson法が増分の大きさによっては収束しにくくなることがあります。そこで、数値震動台では、鋼材の降伏棚とバウシンガー効果を考慮した構成則として、semi-implicitルールを用いて単純なvon Mises降伏条件と線形硬化則を拡張した区分線形複合硬化モデル開発しました。本構成則はＥ－ディフェンスで実施された4層鋼構造骨組の完全崩壊実験の再現解析に適用しています。

鋼材構成則

コンクリート構成則

コンクリート構成則について、前川らによって提案された構成則（以下，前川構成則）を数値震動台に実装しました。前川構成則は、記述は複雑であるものの、コンクリートの非線形挙動を広い範囲に高い精度で表すことに関して高い評価を受けている優れた構成則です。しかし、損傷や塑性変形が進むと歪増分と応力増分の勾配が負となるコンクリートでは、接線剛性行列の正定値性が失われるため、CG法の適用は難しくなります。そこで、非対称・非正定値の弾塑性テンソルの代わりに、対称・正定値の弾性テンソルと補正項を使う形式に構成則を再定式化して、前川構成則を数値震動台に実装しました。また、コンクリートの亀裂の発生・進展を解析する手法としてPDS-FEMを開発しました。連続体力学では、応力・歪の破壊基準が満たされると変位の不連続性として亀裂が発生し、進展します。このような亀裂の発生・進展の解析にはFEMは適していません。FEMは連続性や微分可能性を満たす関数の偏微分方程式の解法であるためです。そこで，連続性や微分可能性を満たさない部分を持つ関数もFEMで扱えるよう、新しい離散化手法として、粒子離散化手法（Particle Discretization Scheme、PDS）を開発しました。 PDSにおいて、変位にはVoronoi分割、変位の一階微分にはDelaunay分割の特性関数を導入しています。特性関数は、ある領域では1それ以外では0という関数であり、不連続性を持ちます。したがって、亀裂の発生・進展をVoronoi分割の境界に限定することで、変位の不連続性である亀裂を扱うことが可能となります。前川構成則とPDS-FEMをＥ－ディフェンスで実施されたRC橋脚の再現解析に適用しています。

また、圧壊を考慮した拡張Drucker-Prager則も数値震動台に実装しています。この構成則はＥーディフェンスで実施された10層RC建物実験の再現解析に適用しています。

高減衰ゴムの構成則

高減衰ゴムは弾塑性的な挙動と粘弾性的な挙動をします。粘弾性モデルについては、弾性部分を超弾性モデルであるOgden体とSimoの粘弾性モデルを採用しています。本構成則はＥ－ディフェンスで実施された高減衰ゴム免震支承の加力実験の再現解析に適用しています。

地盤材料の構成則

土の代表的な弾塑性構成モデルであるClassical critical state modelは2つの実験事実を基礎として導出されています。一つ目は、「正規圧密粘土の体積変化は、初期と現在の有効応力状態で決まり、途中の経路によらない」であり、二つ目は「正規圧密粘土の体積変化は、平均有効主応力の変化によるもの（圧密）とせん断応力比の変化によるもの（コントラクタンシー）から成る」であります。これらの事実より、塑性体積変化が硬化パラメータを意味していることから、塑性体積変化を圧密によるものとコントラクタンシーによるものでモデル化することによって、降伏曲面が導出されます。コントラクタンシーの表現関数に指数関数を用いたものをEC（Exponential Contractancy）モデルといいます。下負荷面モデルは正規降伏曲面の内側に常に相似な形状を持つ負荷面であり、繰返し載荷時のひずみの蓄積や剛性低下を考慮できます。上負荷面は正規降伏曲面の外側に常に相似な形状を持つ負荷面であり、構造劣化による体積圧縮や剛性低下を考慮できます。数値震動台では地盤材料の構成則として上下負荷面を導入したECモデルを実装しました。下負荷面を用いたECモデルは地盤地中構造物実験の再現解析に適用しました。また、液状化問題への適用を視野に入れて、間隙水をダルシー則に基づく非圧縮流体としてモデル化し、土水連成解析モジュールを開発しています。

解析事例

超高層建物

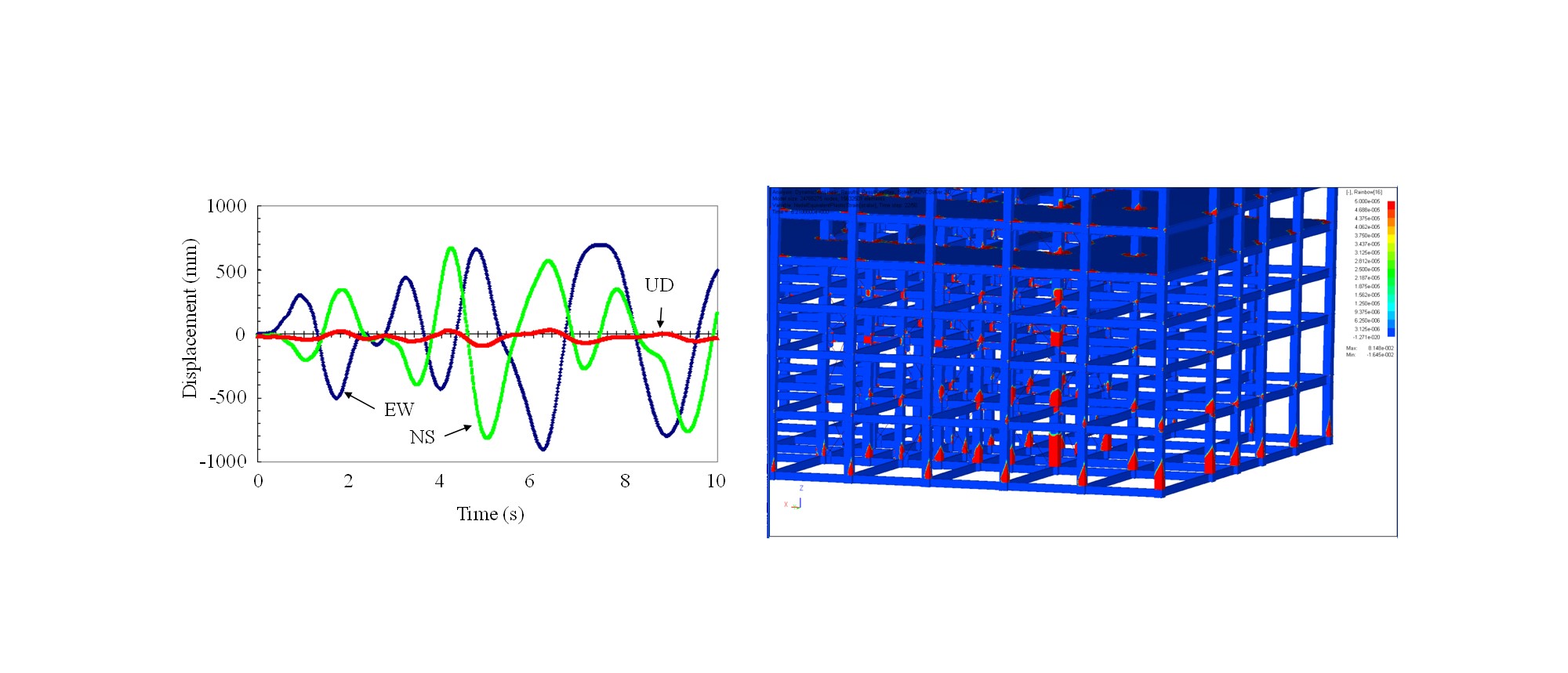
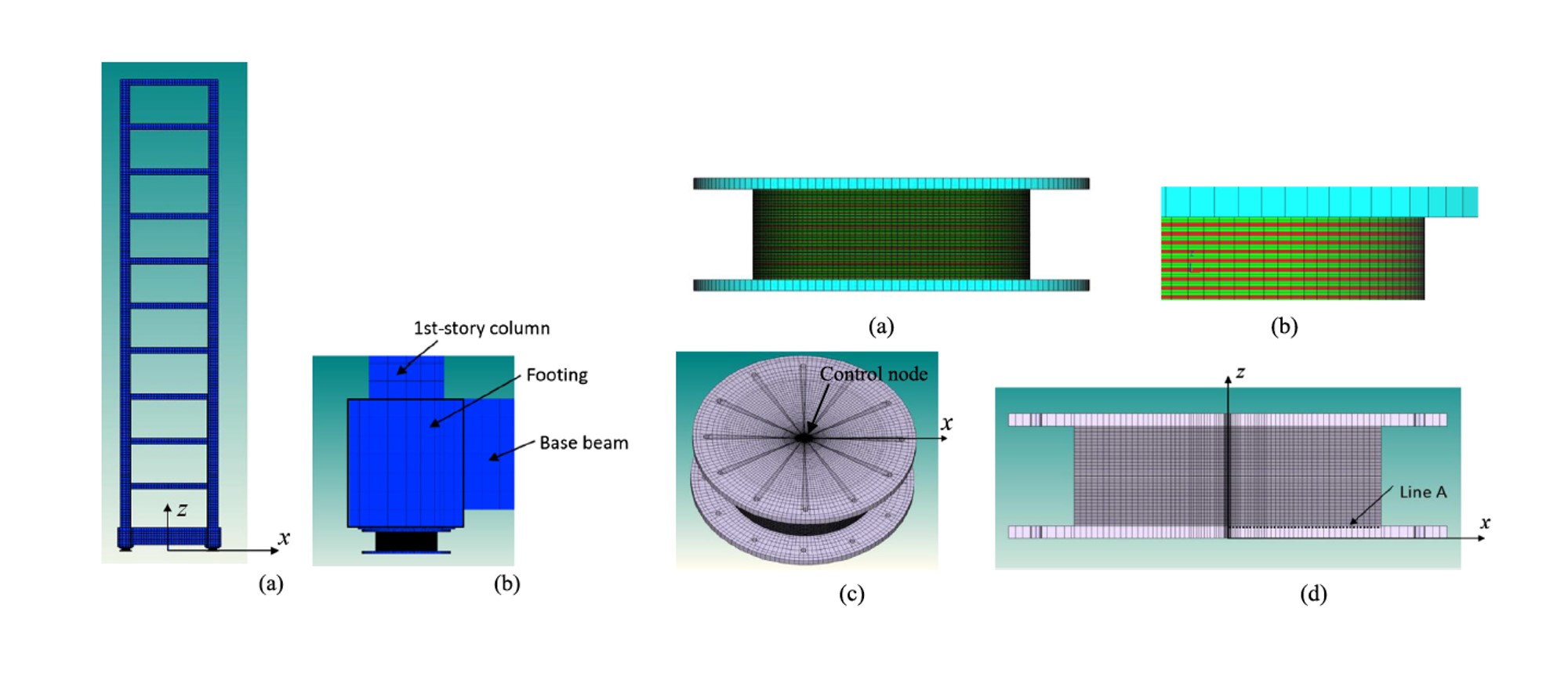
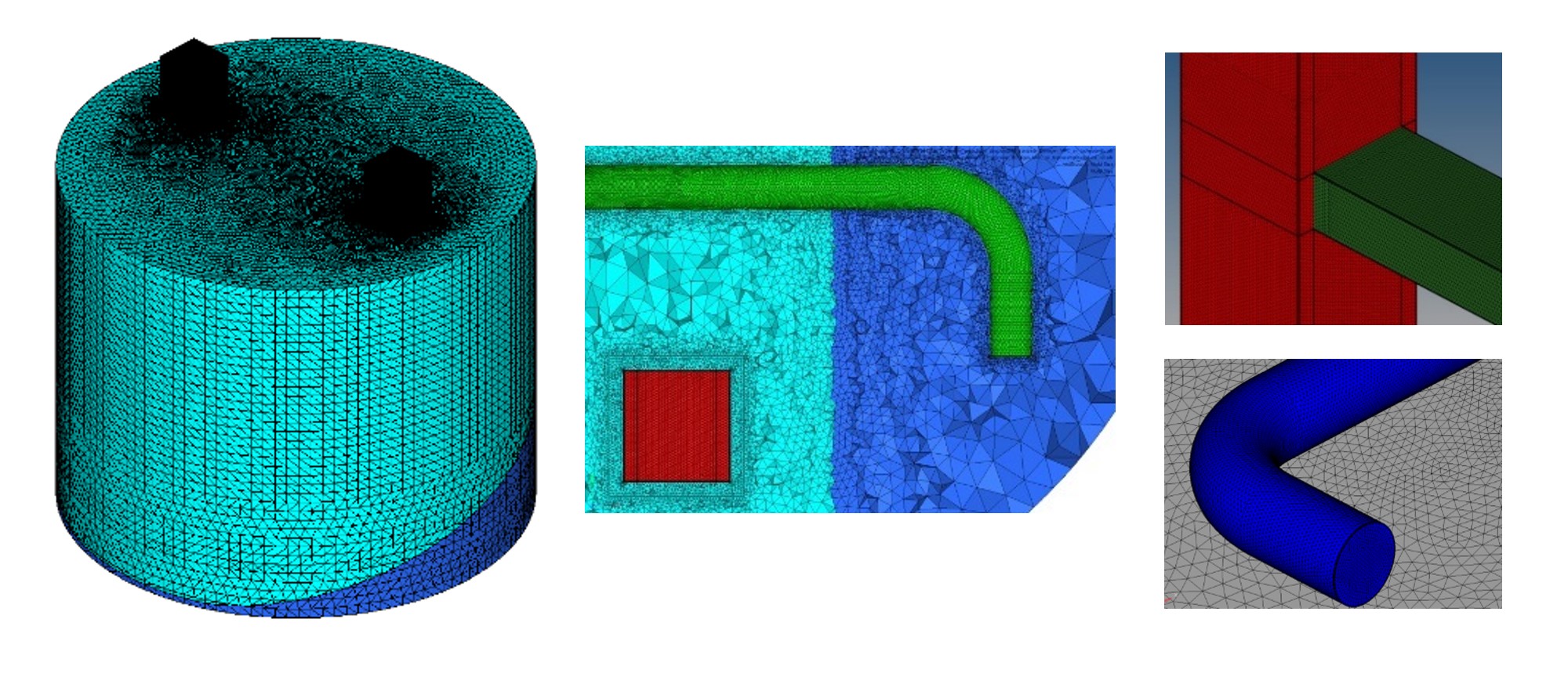
ソリッド要素による詳細メッシュと並列計算手法を用いた建築構造物の大規模解析の実行可能性を検証するために、建築基準法に基づいて設計された31階建のビルを対象とした解析を実施しました。メッシュの規模は、要素数が15,592,786、節点数が24,765,275、自由度数が74,295,825となります。解析モデルとその拡大図を図1に示します。このモデルの底部を固定し加速度の履歴を強制的に与えることで地震波の入力を模擬し解析を行いました。入力波の波形と解析結果を図2に示します。　これらの結果より、ソリッド要素による詳細メッシュを用いた建築構造物の解析と、数千万自由度規模の非線形並列有限要素解析の実行可能性を示しました。

4層鋼構造建物

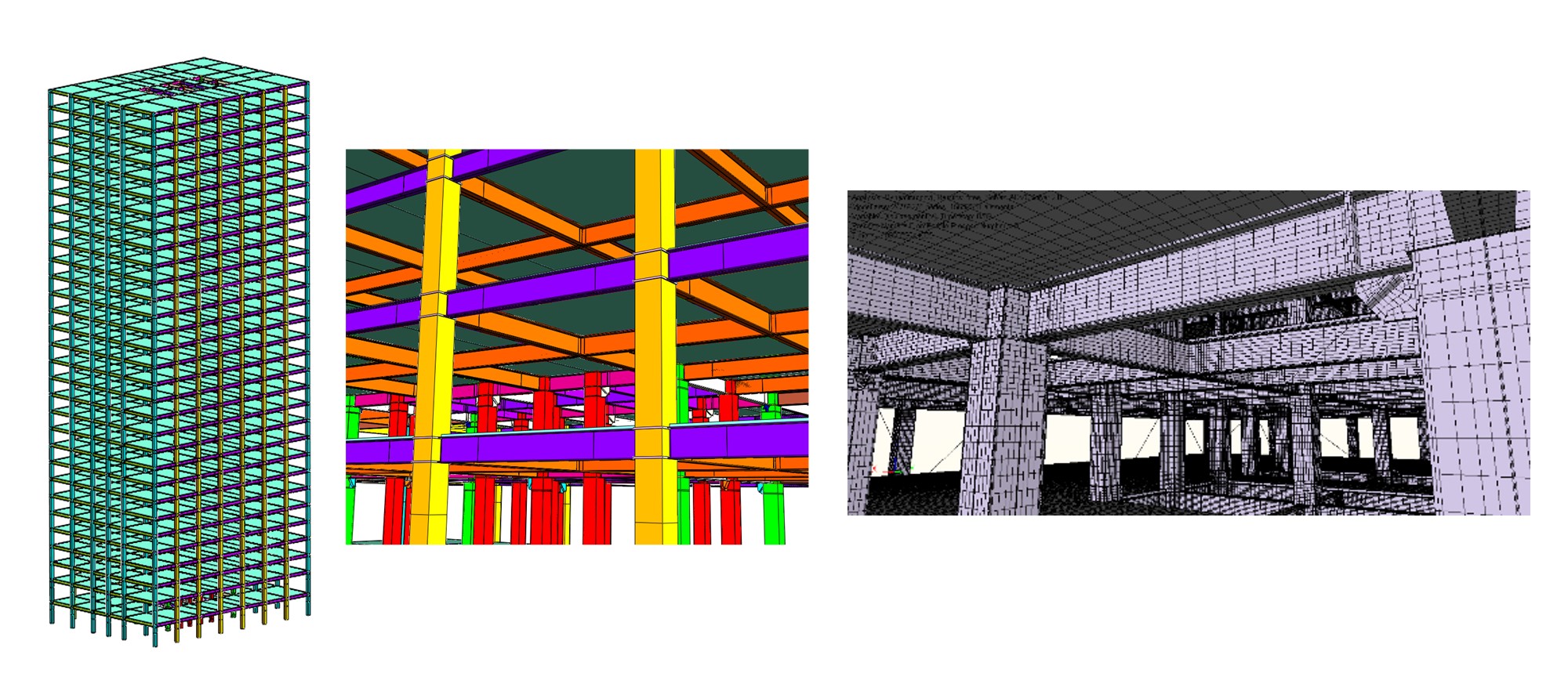
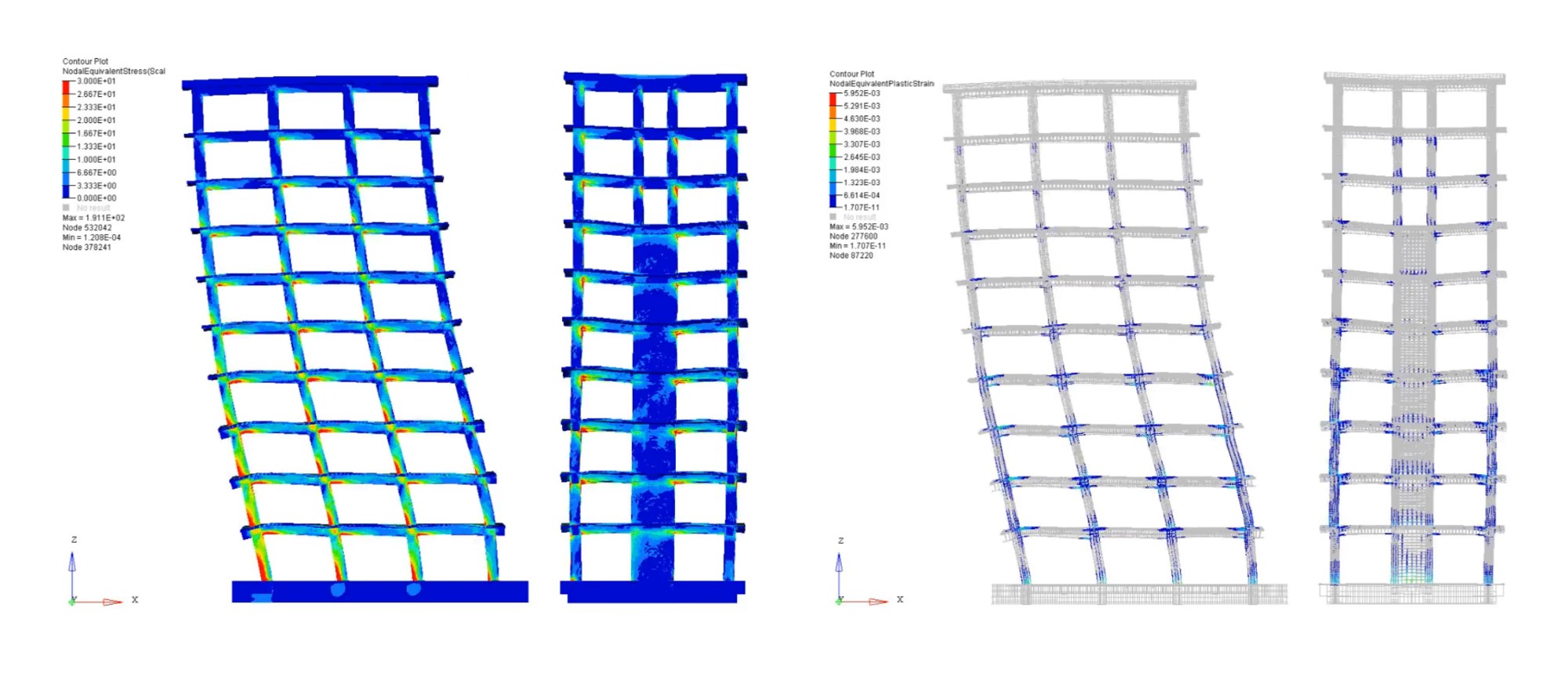
平成19年9月にE-ディフェンスにて実施された４層鋼構造骨組の加振実験の再現解析を実施しました。この再現解析に用いられたモデルを図3に示します。要素数は4,532,742、節点数は6,330,752、自由度数は18,992,256となります。 JMA神戸100％の加振実験を再現解析の対象としました。本解析により、実験において層崩壊の引き金となった，１階柱の上下端の局部座屈の再現に成功しました（図4、図5)

免震建物

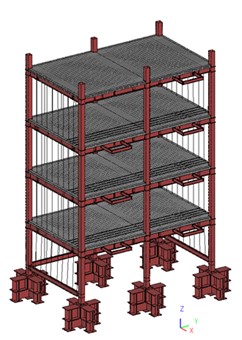
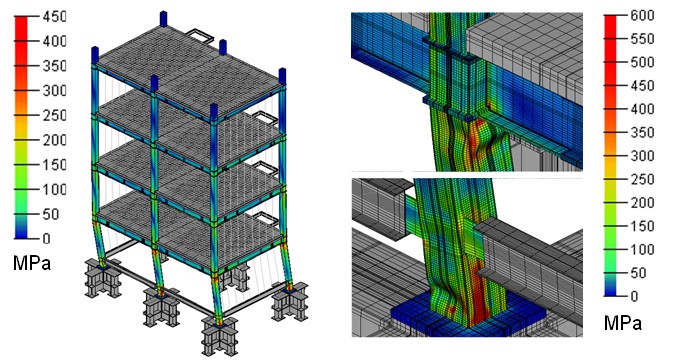
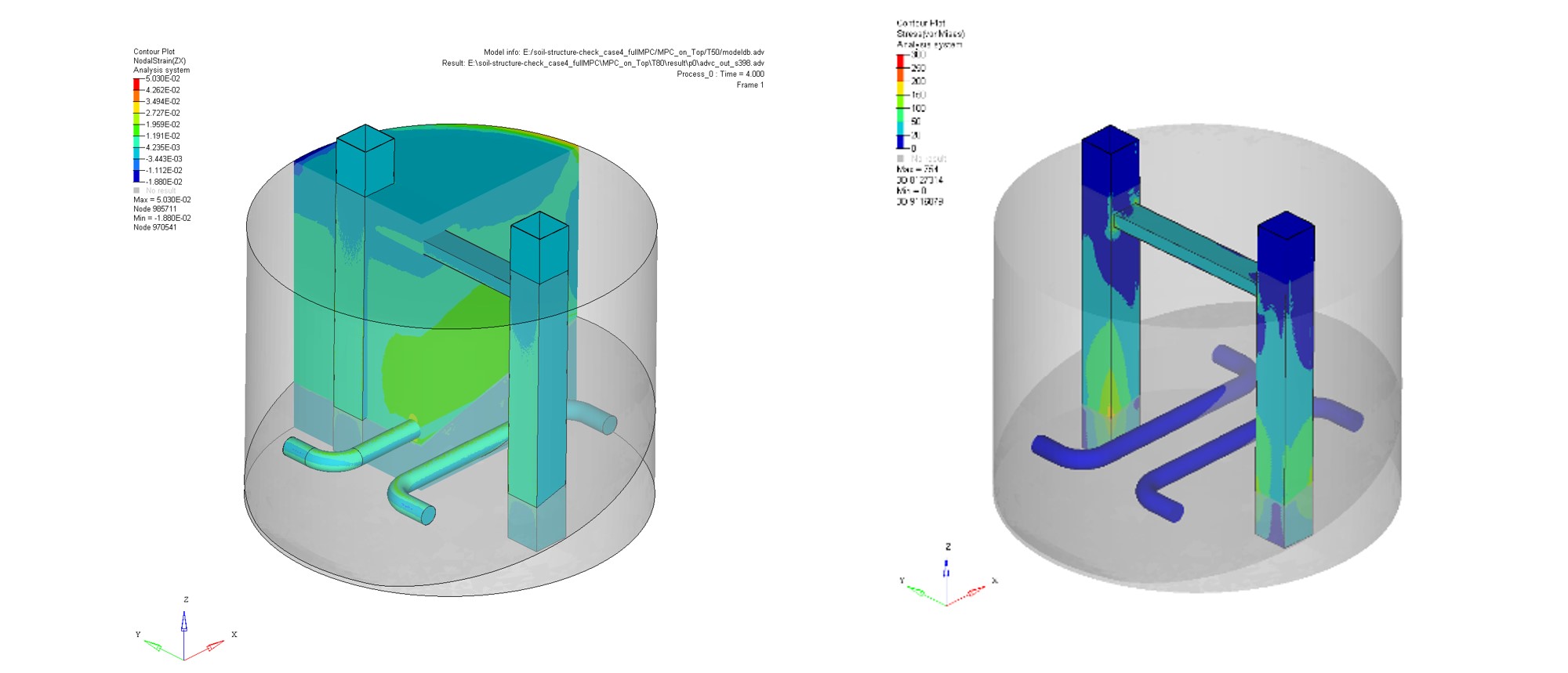
対象とする解析モデルは積層ゴム免震支承を持つ10層のRCフレームモデルです（図7)。積層ゴム免震支承間の距離は7000mm、各階の高さは3500mmです。フレームのヤング率は24.0GPa、ポアソン比は0.2、質量密度は2.3×103kg/m3です。積層ゴムの材料は天然ゴムとしています。ベースの大きさは、1300×1300mm、高さは1500mmとしています。この積層ゴム免震支承の解析モデルの節点は502,981，要素数は，486.240，自由度は1,525,002になります。

天然ゴムは超弾性体モデルの一つであるOgdenモデルと仮定して、体積弾性率は1000 MPa、その他の材料パラメータは、異なる圧力下のせん断応力－ひずみ関係から同定された値を用いています。天然ゴムの密度は，2.00×103 kg/m3としています。境界条件として、BCJ-L2およびAW-神戸波の2種類のレベル2設計用地震動を免震支承底面に入力して、地震応答解析を実施しました。解析の結果、以下の結論を得ました。

約300万の6面体ソリッド要素によりモデル化された、地震動を受ける積層ゴム免震支承建物の解析が可能であることを示しました。
建物と免震支承の連成により、積層ゴム免震支承の上面における鉛直応力の不均一性ならびに局所的な引張応力の発生が確認できました。
水平反力は鉛直反力に強く依存するため、同じ水平変位でもそれぞれの免震支承が受け持つ水平力は異なる値をなりました。

高減衰ゴム免震支承

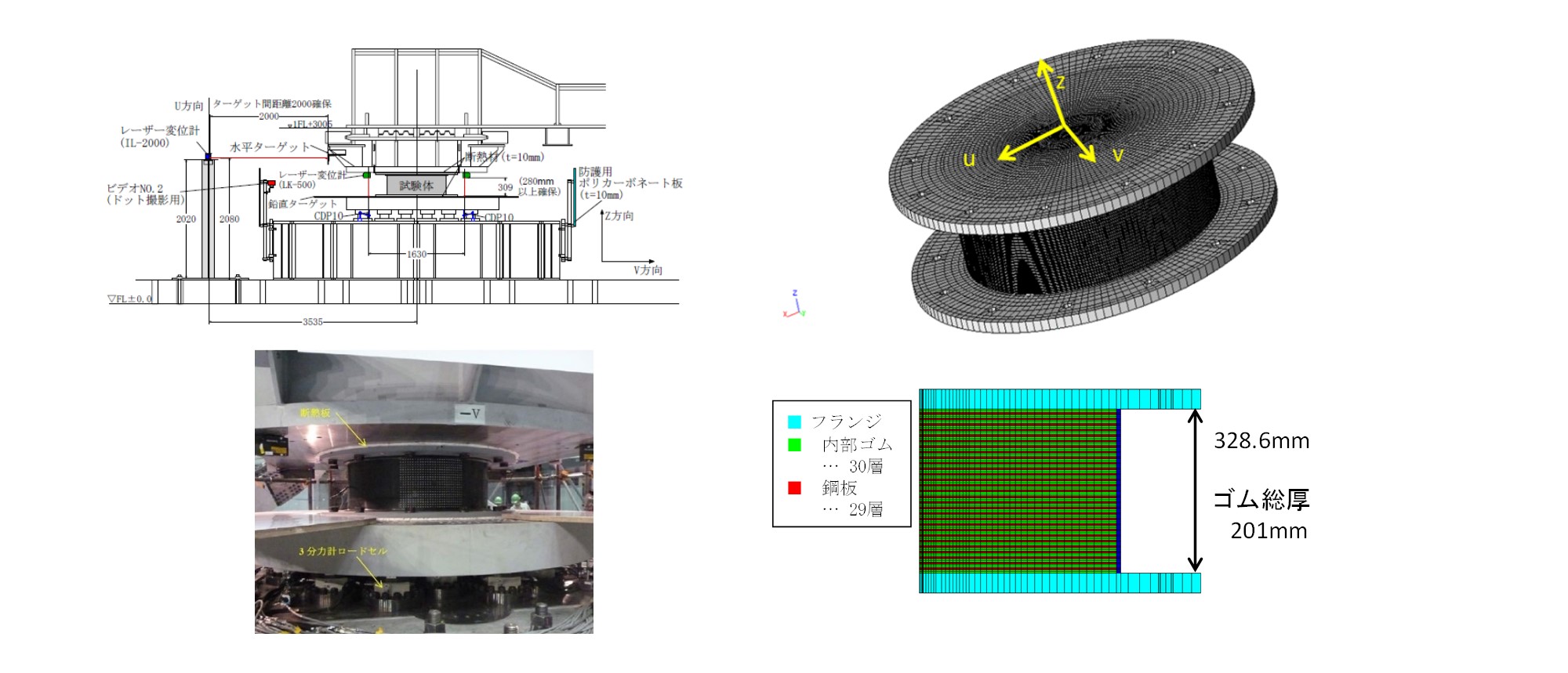
ここでは、E-ディフェンスで実施された実大高減衰ゴム免震支承の加振実験の再現解析事例を紹介します。この実験は、長周期地震動に対する免震建築物の安全性照査のクライテリア設定へ向けて、多数繰り返し加力実験に基づく実大免震支承の特性評価を行うことを目的として実施されました。本解析は、熱連成解析および高減衰ゴムの構成則の妥当性確認のために実施しています。試験体と解析モデルを図8に示します。積層ゴム部の直径は1000mmとなっています。解析モデルの要素数は486,240、節点数は502,981、自由度は1,525,002となっています。熱構造連成解析について、熱伝導解析では、弾塑性、粘弾性材料の発熱を考慮して、時間毎の温度場が求められます。構造解析では、温度による熱ひずみを考慮し、材料の温度依存性は既往の研究で提案された免震支承全体の等価剛性と等価減衰定数に対する温度補正式により考慮しています。

積層ゴム免震支承内の鋼材のヤング率は205.0GPa、ポアソン比は0.3、降伏応力は235.0MPa、線形移動硬化係数は205.0MPa、質量密度は7.86×103kg/m3としています。高減衰ゴムは弾塑性的な挙動と粘弾性的な挙動をします。そこで、弾塑性モデルと粘弾性モデル（弾性部分を超弾性体モデルであるOgden体としたSimoの粘弾性モデル）を並列にしています。 Simoの粘弾性モデルは超弾性ばね、ダッシュポットとばねを直列に接続したMaxwellモデル2個を並列に置いたものです。また、高減衰ゴムの材料パラメータは1方向正弦波加振実験の結果から同定しています。解析は、水平1方向正弦波加振と水平2方向繰返し楕円加振の2種類の解析を実施しました。境界条件として、鉛直方向の面圧は5 N/mm2とし、水平1方向正弦波加振では、強制変位をｖ方向に与えました。

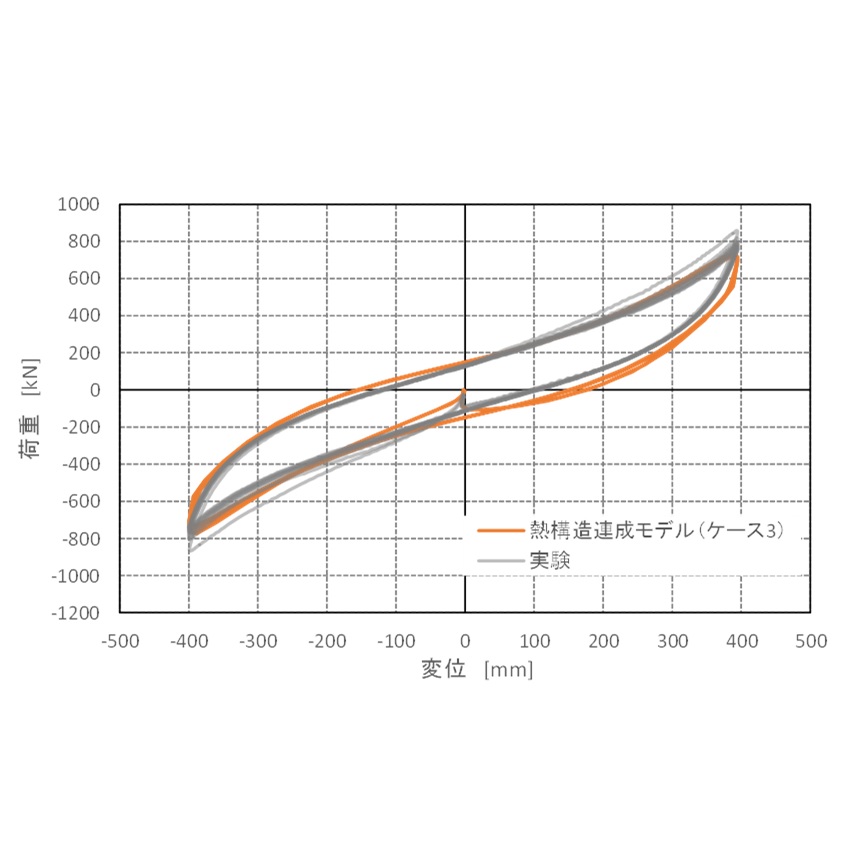
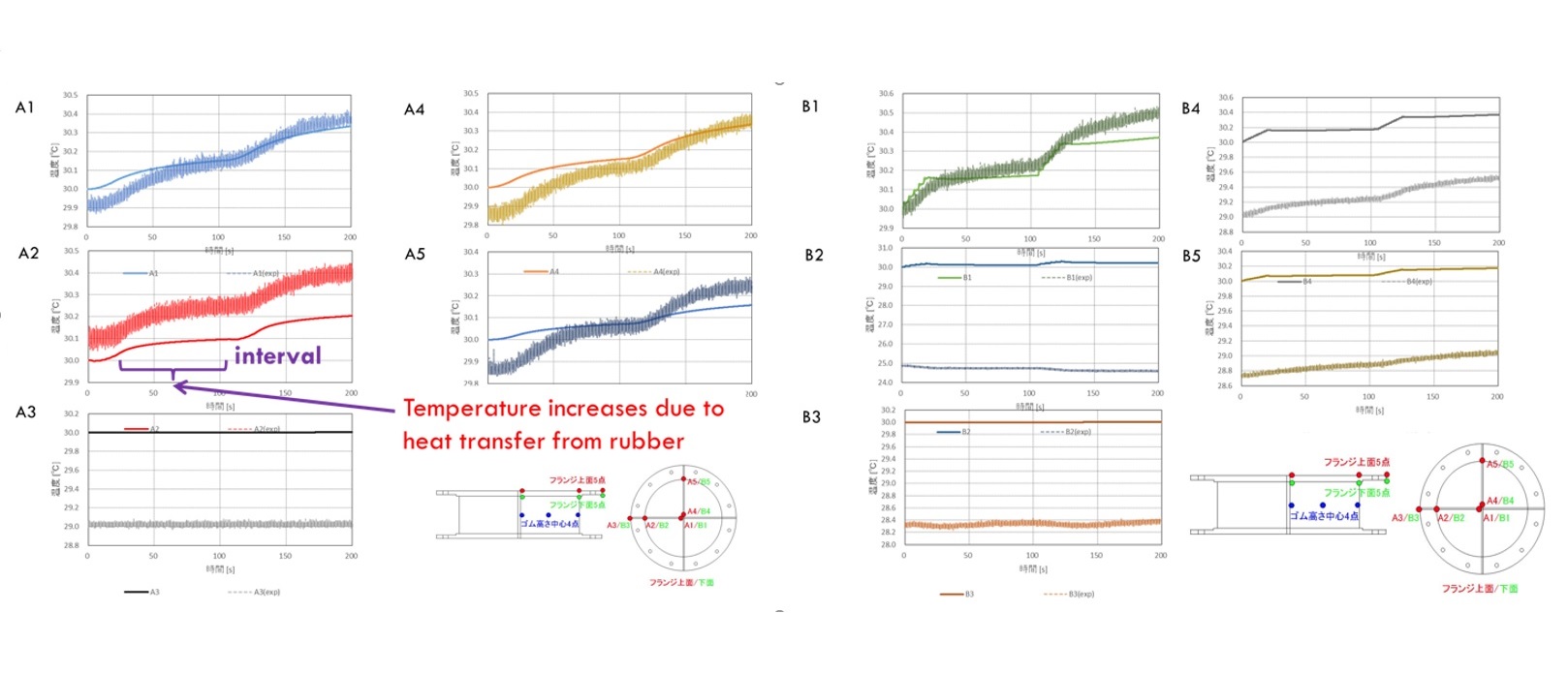
水平1方向正弦波加振での実験と解析において得られた水平面における荷重と変位の関係を図9に示します。図より、解析の荷重―変位関係が実験と概ね一致することが確認できました。フランジ上面と下面の温度変化を、図10に示します．これらの結果より、高減衰ゴムにおける繰り返し加振による温度上昇が確認できました。

10層鉄筋コンクリート造建物

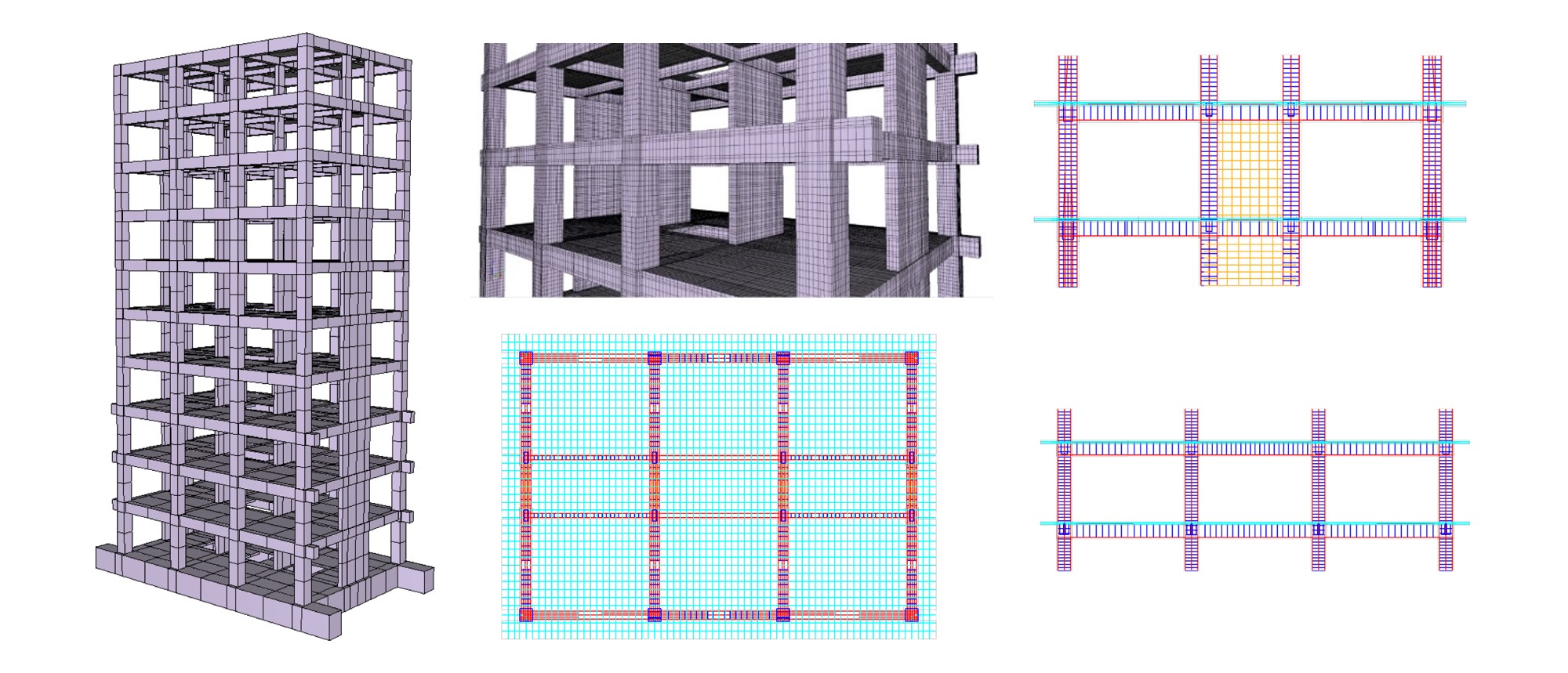
平成27年にＥ―ディフェンスにおいて、現行基準で設計された10階建てRC建物の震動台実験が実施されました。この実験の主な目的は、大地震後の継続使用が可能となる建物の技術的知見の取得、各部材の損傷過程の把握、骨組の損傷や応答の評価です。数値震動台では、RC骨組建物を対象とした解析技術開発のため、本実験の試解析を実施し、実大実験との比較により解析の高度化のための課題抽出を行いました。本解析では、図11に示す解析モデルを用いて解析を行いました。 6面体ソリッドメッシュで作成されたモデルの規模は、要素数1,997,689、節点数1,652,041、自由度4,956,123となります。 JMA神戸100％の加振実験を解析の対象としました。

加振時のコンクリートと鉄筋の変形と相当塑性ひずみ分布を図12に示します。コンクリートにおいては、各階の床の柱および柱の接合部においてひずみが集中していることが確認できます。また、鉄筋においては、接合部付近を中心にひずみが集中していることが確認できます。

地盤地中構造物

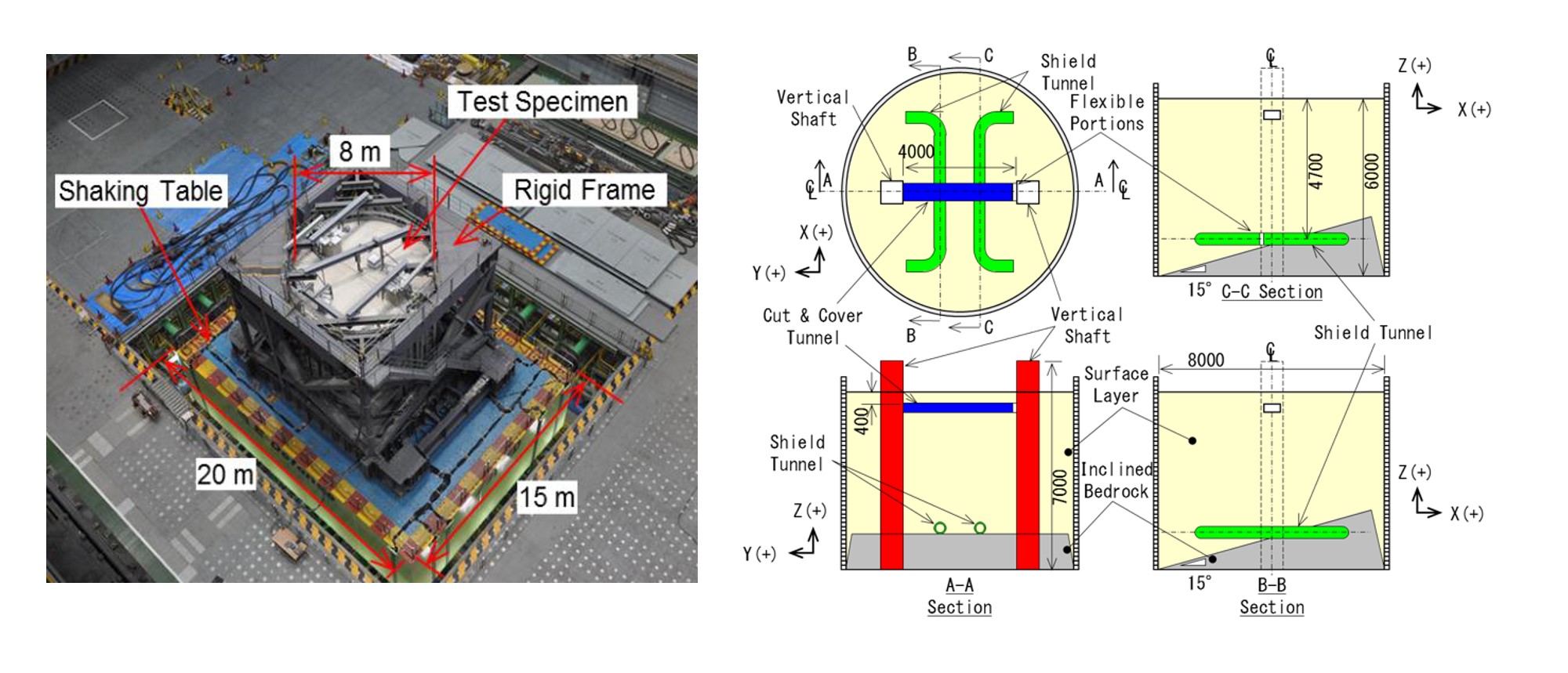
平成24年2月にE－ディフェンスで実施された地盤地中構造物実験の再現解析を紹介します。本実験は、大型の地盤地中構造物が大地震を受けた際の構造物の連結部分や硬い地盤と軟らかい地盤の境界付近での局所的な挙動や破壊に至るメカニズムの解明を目的として実施されました。本解析では、再現解析を通して解析モデルの検討および境界条件の設定、地盤構成則の検証を行っています。図13に対象となる試験体の詳細を、図14に解析モデルを示します。

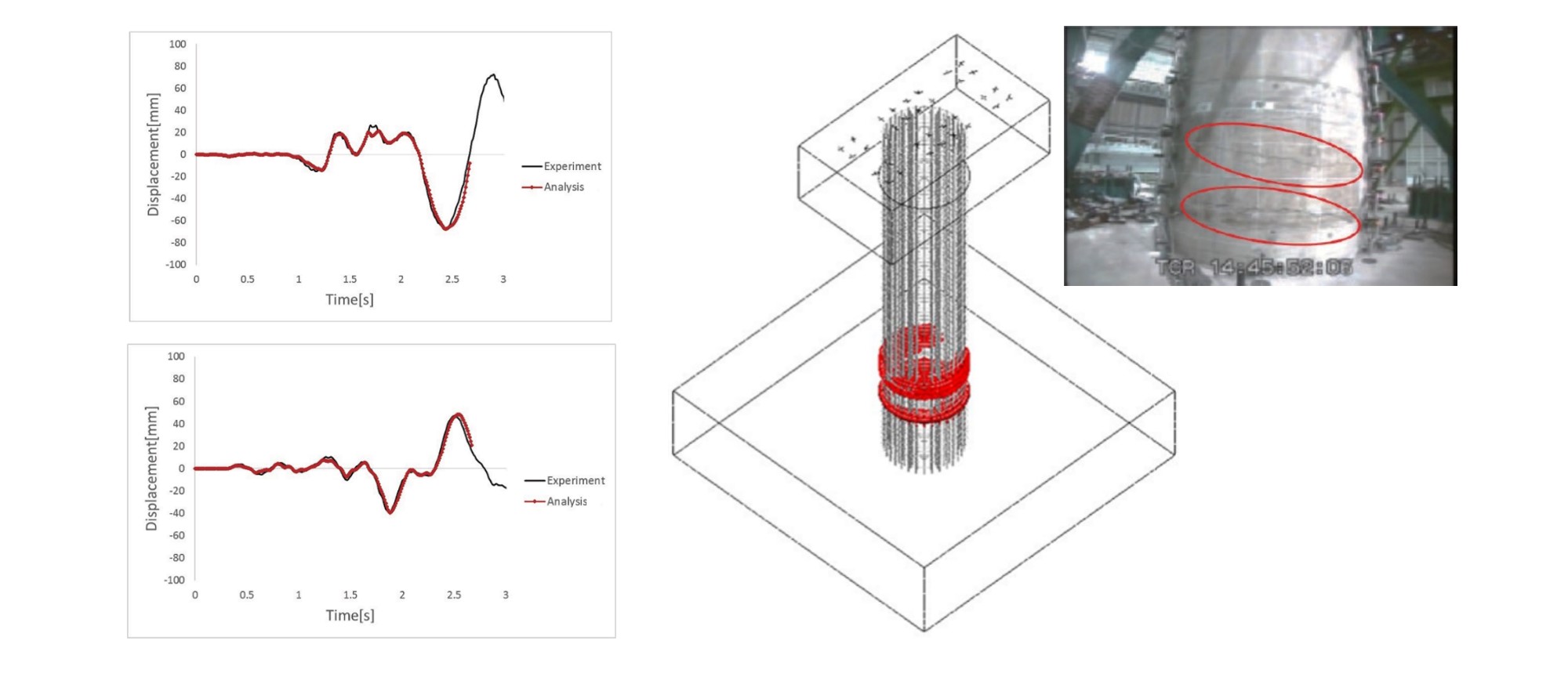
材料試験結果から求められたパラメータを用いて、弾塑性解析を実施しました。地盤上面の応答変位ならびに応答加速度を実験結果と比較して、比較的良好に再現できていることを確認しています。応答変位については、残留変形の再現性が今後の課題となっています。

鉄筋コンクリート橋脚

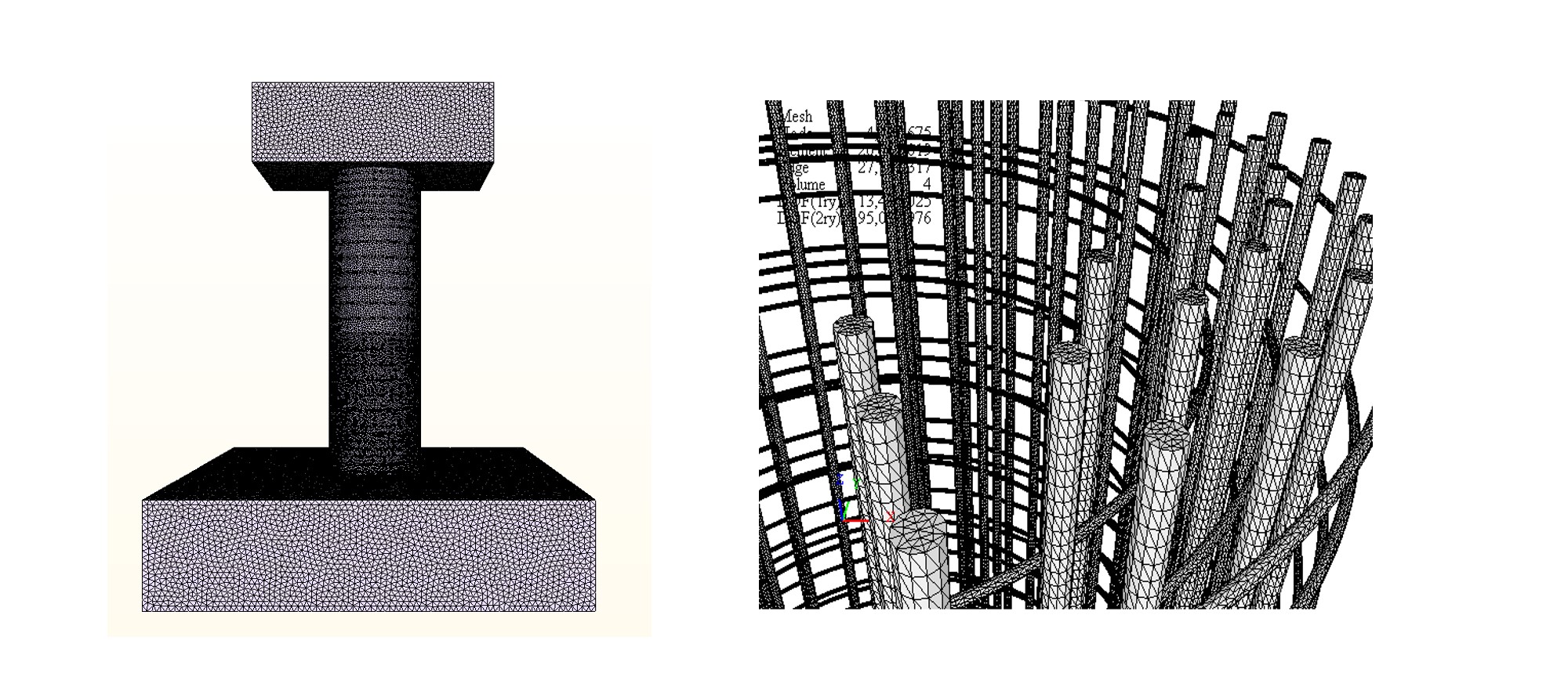
平成19年12月にE-ディフェンスで実施された鉄筋コンクリート（RC）橋脚実大震動台実験の再現解析について紹介します。本実験は、1970年代に建設された曲げ破壊先行型のRC橋脚の履歴特性、破壊特性を研究対象としています。使用した試験体は、直径2m、高さ7.5mの大型円形断面RC橋脚です（図16）。数値震動台では、この破壊形式を再現するために、前川構成則およびPDS-FEMを開発、実装して再現解析を実施しました。 RC橋脚の解析モデルを図17に示します。解析メッシュは、コンクリート、鉄筋とも4面体のソリッド要素で作成しました。この解析モデルに対して、JR鷹取波を入力加速度として与えました。また、対象としているのは橋脚のみであるため、橋桁からの影響については橋脚上面のロードセルによって計測された反力を荷重境界条件として与えました。

x方向、y方向の変位について、実験と解析との比較を図18に示します。黒および赤の実線は、それぞれ実験および解析による応答変位です。この結果より、良好な一致が確認できます。図中には、鉄筋の近傍でのコンクリートの亀裂進展も併せて示しています。亀裂進展の状況も、実大実験と対応しています。コンクリート材料のモデル化として前川構成則とPDS-FEMを用いることにより、実験を良好に再現する解析結果を得ることができています。

室内被害を再現するシミュレーション技術の開発

プログラムの概要

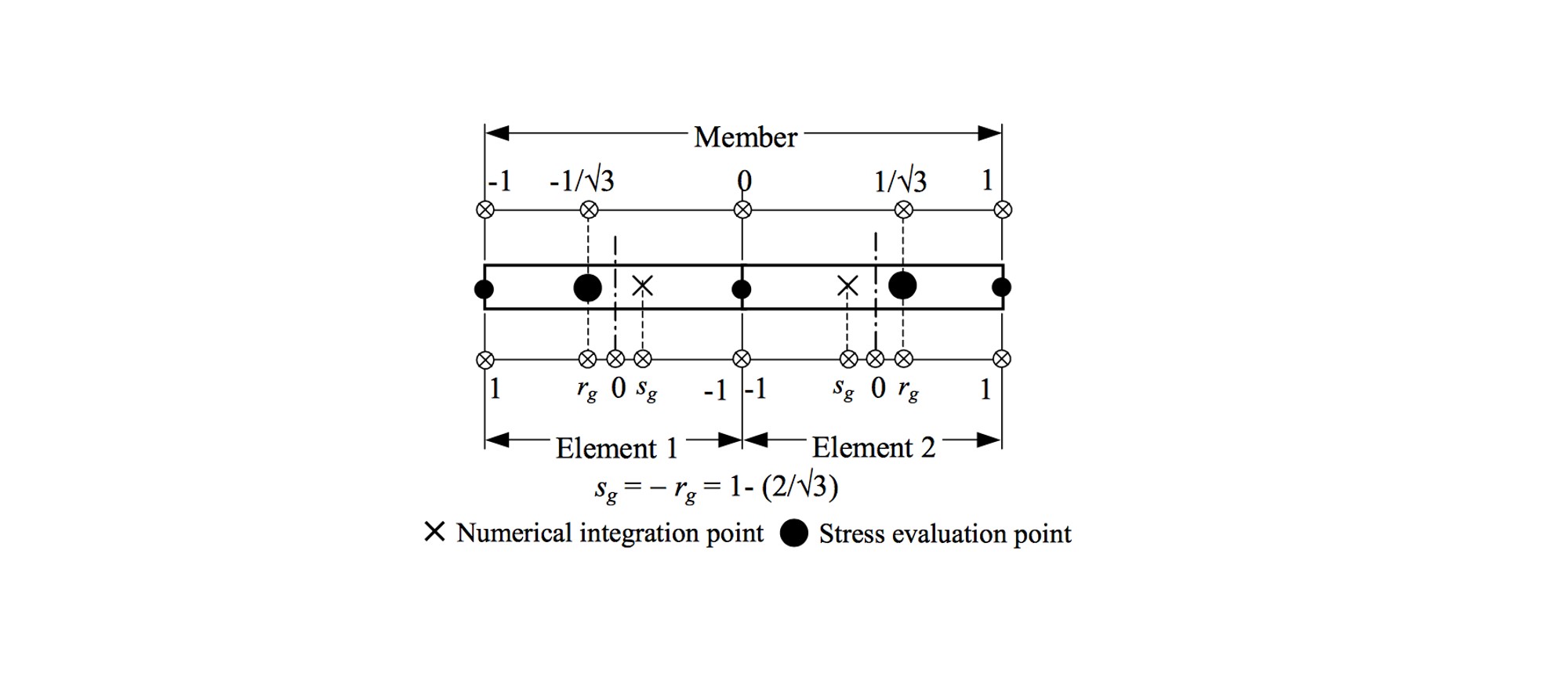
室内被害の再現には、ASI-Gauss法という手法を用います。 ASI-Gauss法とは、解析対象の要素内の数値積分点を部材形状に応じて順応的にシフトすることで、計算コストを低く抑えることが可能な順応型Shifted Integration (ASI法)を改良した手法です。 ASI-Gauss法では、ASI法での欠点がある弾性域で精度が落ちるという問題を解消しています。接触問題に関してはペナルティ法を用いています。

ASI-Gauss法では、図2-1のように2つの線形チモシェンコはり要素をサブセット要素とし、3次はり要素と同様にガウス積分点に相当する応力評価点を配置します。これは、2つの線形チモシェンコはり要素を用いて、2点積分法に基づいた1つの要素を模擬することに相当します。ガウス積分点で評価される曲げの変形精度が数学的に保証され、その点が2点積分法における最適な積分点の位置であることを利用しています。

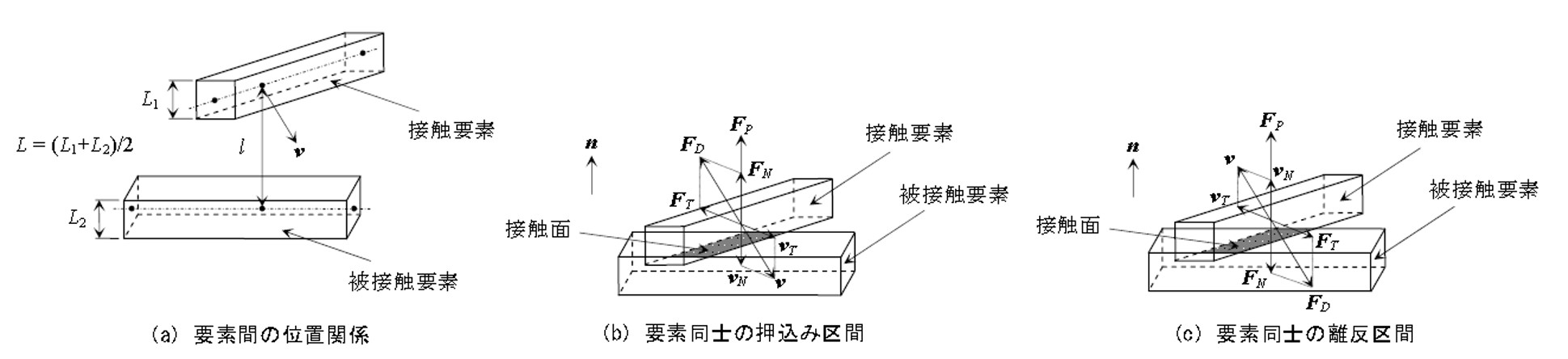
接触が判定された2つの要素には、ペナルティ接触理論に基づく接触アルゴリズムを用いて接触力や摩擦力を作用させます。図2-2(a)に示すように2つのはり要素を考えます。部材幅L₁を持つ接触要素が部材幅L₂を持つ非接触要素に対し、相対速度vで移動しているものとします。要素の節点の幾何学的位置関係によって接触が判定された際に図2-2(b)に示すように要素間に2種類の接触力F_P，F_Dが作用することになります。 F_Pはペナルティ力であり、接触面の法線方向にのみ作用します。 F_Pの方向は要素同士の押し込み区間（図2-2(b)），離反区間（図2-2(c)）で違いはなく常に一定の方向を向いています。

解析事例

家具の地震時挙動

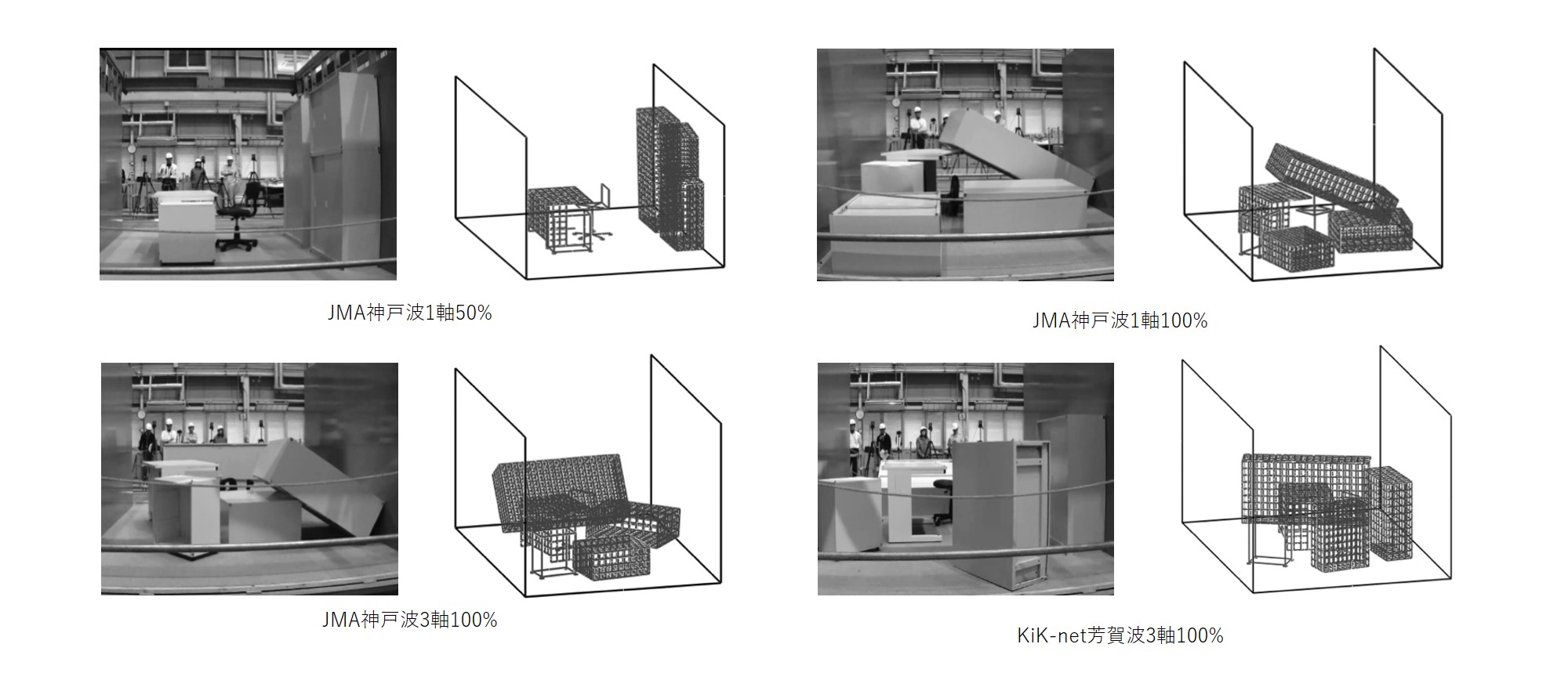
オフィスを想定した家具を振動台上に設置し、地震波が入力されたときの家具の3次元挙動を測定しました。家具の挙動は、モーションキャプチャシステム（以下，MCSとする）を用いて測定しました。家具の配置は図2-3に示す3種類としました。 MCSにより計測された3次元挙動と解析による結果を比較し、地震入力を受ける家具の地震時挙動の再現解析の精度向上と解析の妥当性確認を行いました。

図2-4に配置3の実験および解析終了時の家具の様子を示します。異なる地震波の入力条件の場合でも接触の条件は全て同じとしているが、いずれの場合でも家具の位置および姿勢が実験と解析で酷似していることが確認できます。

医療施設のキャスター付き什器の地震時挙動

兵庫県南部地震では、大地震による医療施設での什器の破損や故障によって、医療活動が困難となりました。医療施設では、利便性の観点からキャスター付什器が多数されています。これらの地震時挙動を把握することは室内の安全性の検討に役立ちます。平成20年にＥ－ディフェンスにおいて実施された医療施設での加振実験により得られたデータを基に、医療什器の加振挙動解析を実施しました。キャスターの固定状態を変化させるため、動摩擦係数を操作する手法を取り入れ、キャスターの固定状態が什器に及ぼす影響について検証しました。

解析に用いた什器の数値モデルを図2-5に示します。解析の入力加速度として2種類の波形を用いました。一つ目は、実験において耐震構造に短周期地震動であるJMA神戸波80%を3軸方向に入力した際に手術室で計測された床応答加速度（以下，耐震-短周期）です。二つ目は、実験において免震構造に長周期地震動である三の丸波100%を水平2軸方向に入力した際に手術室で計測された床応答加速度（以下，免震-長周期）です．

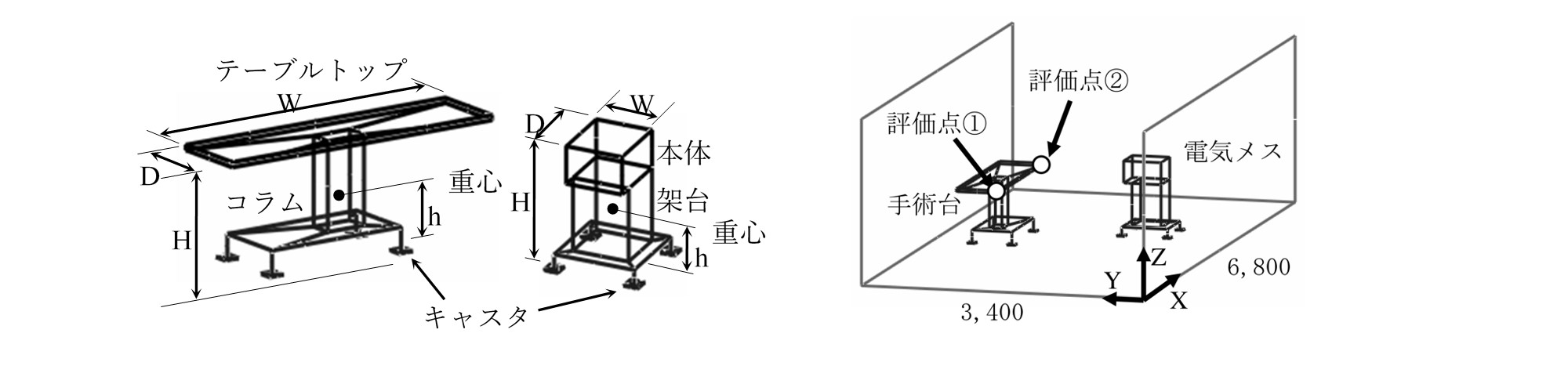
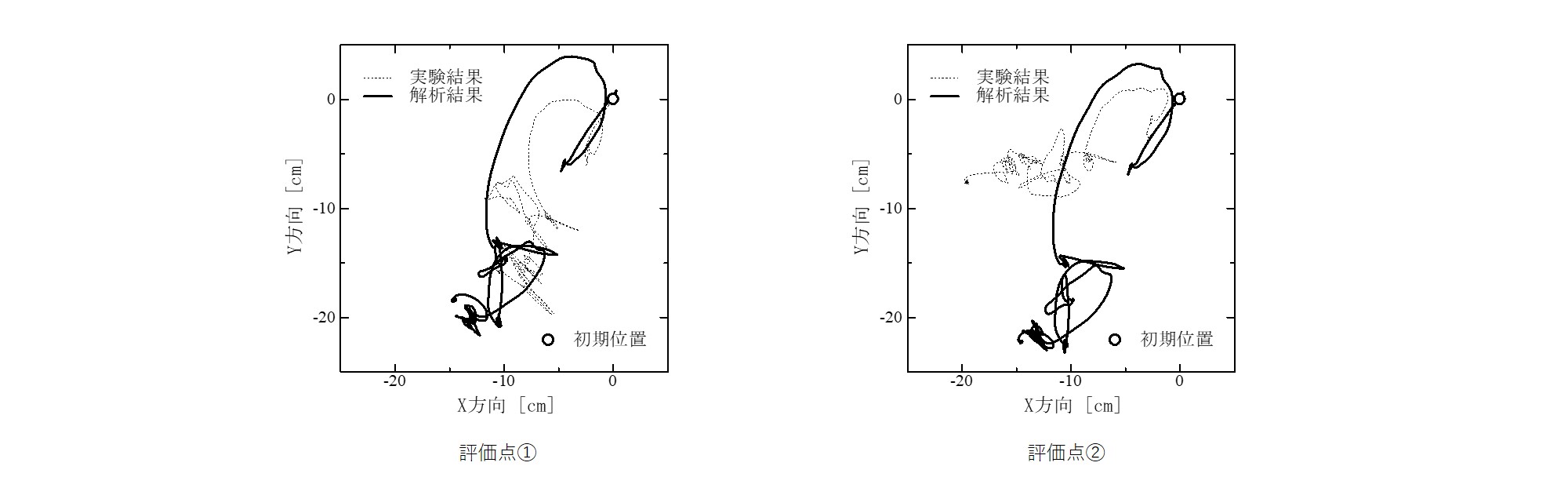
キャスターを完全ロック、キャスターの首振りは自由、手術台の高さ760mmの際の実験と解析の比較を図2-6に示します。図2-5内の評価点①，②の軌跡を表しています。評価点①では移動方向・移動距離ともに概ね一致しています。評価点②では、移動距離は概ね一致していますが、移動方向のずれがみられます。キャスターの方向が不明確であることを考慮すると、解析結果は移動距離に関して妥当性のある結果を得ることができています。

吊り天井付き体育館の地震時挙動

大地震時に避難施設としての役割を持つ体育館などにおいて、天井材等の落下被害の事例が報告されている。平成26年にＥ－ディフェンスにおいて、吊り天井を有する体育館を模擬した試験体による吊り天井脱落被害の再現実験が実施されました。実験において観察された吊りボルトやブレースの座屈現象を考慮して、天井モデルを有する体育館の解析を実施しました。

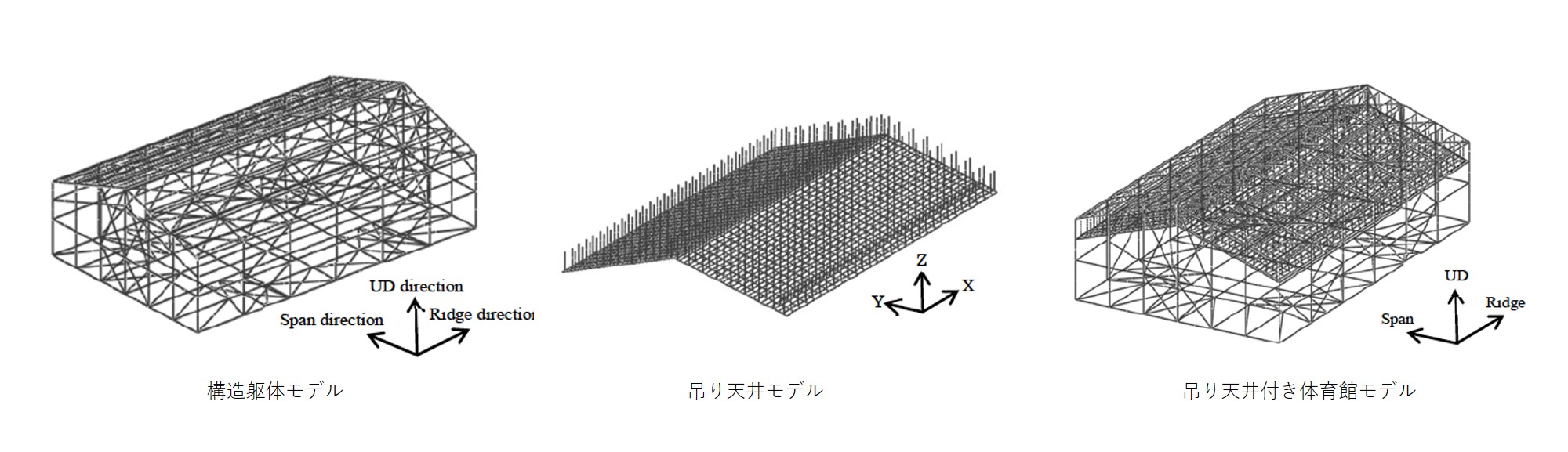
Ｅ－ディフェンスでの実験に使用された実大体育館試験体に基づいて、体育館の構造躯体モデルを作成しました。体育館は鋼構造の平屋建てです。平面寸法は、桁行30.0m×梁間18.6mであり、屋根勾配は10:3，最大高さは9.09mです。全ての構造部材は、基本的に1部材当り2つの線形チモシェンコはり要素でモデル化しています。大梁、小梁およびブレースは両端がピン接合であるため、部材両端に曲げ剛性を低下させた微小要素（長さ：他要素の1/2,剛性：部材剛性の1/10,000）を追加しています。ブレースは座屈現象の再現を可能とするため、10要素で分割しています。大梁上に取り付けた屋根面重量を模擬するためのおもりやキャットウォークは、重量のみを考慮し大梁に密度として加えています。引き抜き力によるアンカーボルトの伸びを考慮するために、柱脚部には回転剛性を低下させた微小要素を配置しています。

吊り天井を構成する部材は、吊りボルト、野縁受け、野縁、せっこうボードクリップ、ビス、野縁ジョイントです。吊りボルトの長さは、1,500mm、クリップ、ビスの長さは25mm、野縁ジョイントの長さは2mmとしました。吊りボルトとハンガーは一体化してモデル化しました。解析モデルを図2-7に示します。吊り天井付き体育館モデルは、全要素数が37,518、全節点数が30,059となります。

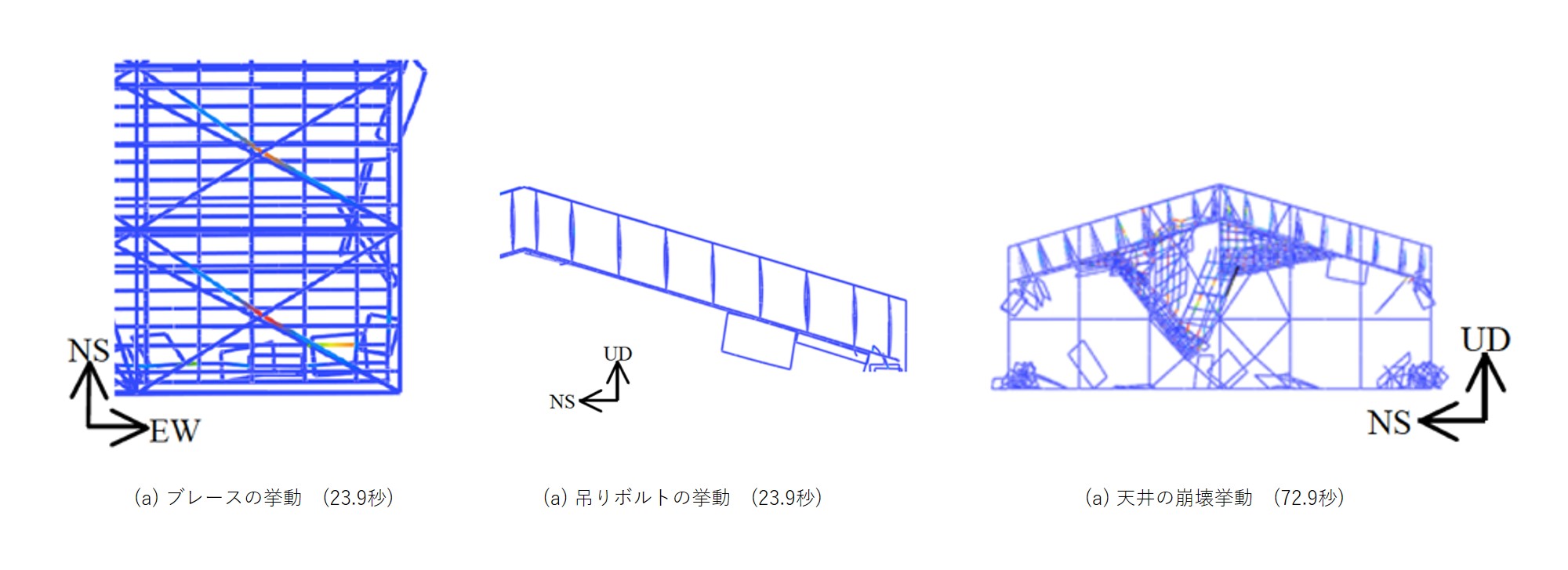
実験と解析の屋根面の時刻歴の変位応答の比較を図2-8に示します。位相や振幅が良好に一致していることがわかります。図2-9(a)に屋根面ブレースの挙動を図2-9(b)にブレースの挙動を示します。図より、屋根面ブレース中央部に塑性座屈が見られ、吊りボルトに鉛直方向の地震動に起因する座屈変形が見られます。図2-(c)に天井落下挙動を示します。頂部中央付近で、クリップが破損し、野縁とせっこうボードが一体となり宙吊り状態となりました。その宙づりになった天井の上下方向の揺れにより、野縁と野縁受けを繋ぐクリップが破損し、連鎖的なクリップの破損が生じました。野縁とせっこうボードの一体となった落下現象が見られました．